Comunemente si ritiene che la Geometria sia la scienza che studia lo spazio, e gli oggetti in esso contenuti, in quanto hanno una "estensione"; la stessa etimologia del termine "Geometria" sembra sostenere questa ipotesi, visto che deriva dalle fusione di due parole che in greco significano "terra" e "misura", col che la Geometria dovrebbe essere la misura dei terreni! Certamente si può immaginare che la prime nozioni geometriche siano state elaborate per scopi pratici, come appunto la misura dei terreni, ma se la nostra scienza si riducesse a questo, certo non desterebbe in molti l'interesse che ha acceso negli ultimi duemilacinquecento anni. Tradizionalmente si fa risalire la nascita della Geometria come la intendiamo oggi, a uno dei sette savi: Talete. Fu lui che per primo immaginò i punti, le rette e i piani dello spazio. Li immaginò, perché, da allora in poi, i punti, le rette ed i piani non furono più entità materiali, ma astratte, idealizzate, impercettibili se non con gli occhi dell'immaginazione. Così per i Greci, il punto è ciò che non ha parte, la retta è lunghezza senza larghezza, e così via.
Il concetto di estensione non è quindi più sufficiente a descrivere le figure geometriche, ed al suo posto, vennero introdotti dei concetti astratti sui quali poter lavorare in modo logico, sintetico, ragionando cioè per dimostrazioni e deduzioni, anziché "a vista" come empiricamente si faceva prima di Talete. Euclide, il grande sistematore della Geometria greca, elaborò in modo completo questa concezione, e la sua opera, i famosi Elementi, gli sopravvisse di molti secoli: in effetti il metodo ipotetico-deduttivo costituisca da allora l'ossatura tipica della matematica, ed è il motivo del suo successo; si fissano dei principi ritenuti "evidenti" (il termine che si riferisce al senso della vista dimostra come la Geometria sia stata la prima ad essere sistemata in questo modo) e, usando le regole di deduzione logica, si deducono da essi teoremi sempre più complicati, dando vita ad una catena potenzialmente infinita di informazioni certe. Per questo carattere di universalità e certezza, la Geometria greca parve alle civiltà seguenti (romana, islamica e medievale) così perfetta da meritare solo dei commenti e degli elogi, e, di fatto, lo sviluppo della Geometria può dirsi inesistente per tutto i due millenni che separano i Greci dal Rinascimento.
Il concetto di spazio e di Geometria ereditato dall'antichità era, come si è detto, idealizzato, ma certo nessuno degli antichi dubitava che "le cose", cioè tutto ciò che vi è nell'universo, fossero suscettibili di descrizione geometrica che, insomma, la Geometria fosse la scienza dello spazio, intendendo con ciò anche l'universo stesso (che infatti veniva creduto per lo più composto di sfere...). E questa concezione è molto diffusa anche oggi.
La grande rivoluzione nella Geometria fu quella di Cartesio, che mostrò come si potessero sostituire i complicatissimi argomenti deduttivi delle dimostrazioni euclidee, e le spesso perverse costruzioni geometriche (che forse molti di noi hanno detestato al liceo) con semplici calcoli su numeri che rappresentassero i punti, le rette, i piani... introducendo il concetto di coordinate e la Geometria che porta il suo nome. Non è erroneo paragonare questa scoperta alla rivoluzione copernicana in astronomia: infatti questa nuova concezione dischiuse possibilità inimmaginabili fino ad allora. Il motivo sta nel fatto che il metodo sintetico (basato cioè sulla deduzione logica) ormai esplorato in tutte le sue direzioni veniva soppiantato dal metodo analitico, che consentiva di tradurre le leggi geometriche in equazioni e quindi di calcolare le traiettorie e le posizioni degli oggetti geometrici piuttosto che costruirle: questo, ad esempio, consentì a Newton di formulare le sue teorie meccaniche e astronomiche in modo conciso ed elegante e diede origine al filone di ricerche poi sfociato nell'Analisi matematica (che trae il suo nome proprio da questa origine). L'introduzione della Geometria Cartesiana fece pensare che l'universo fosse in qualche modo controllabile, nei suoi moti e nelle sue distanze, proprio per mezzo delle coordinate che Cartesio aveva introdotto nella Geometria Euclidea.
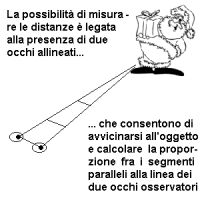
La Geometria Euclidea e Cartesiana sono basate sul concetto di distanza: cioè considerano equivalenti due figure se queste possono essere trasportate una sull'altra (in modo da sovrapporsi: ricordiamo che gli oggetti della Geometria sono immateriali, come proiezioni cinematografiche o olografiche) per mezzo di movimenti "rigidi" cioè che conservino le distanze reciproche fra i punti delle figure che vengono spostate. Che la Geometria della "distanza" sia la più naturale è un fatto che ogni antropologo può spiegare: noi infatti, intesi come specie umana, siamo "scimmie antropomorfe" (non sembrerà un complimento ma è così), apparteniamo cioè a quella famiglia di animali che hanno, fra le altre cose, due occhi allineati sotto la fronte, che possono cioè valutare con lo sguardo le distanze (sarebbe tragico il viceversa: una scimmia non potrebbe saltare da un ramo all'altro senza spiaccicarsi al suolo...) e questa possibilità rende estremamente naturale per noi il concetto di distanza e quindi la Geometria Euclidea.
Ancora nel diciottesimo secolo, il grande filosofo tedesco Immanuel Kant poteva scrivere che la Geometria Euclidea è data a priori, che si tratta cioè dell'unico modo possibile di concepire lo spazio, che per Kant è un concetto trascendentale, e precisamente una forma della nostra percezione e non un dato oggettivo in sé (e questa è una visione di grande modernità). Pochi anni dopo questa concezione venne radicalmente confutata dalla nascita delle cosiddette geometrie non euclidee; l'errore di Kant originava dalla sua necessità di cercare un fondamento universale, rispetto alla ragione umana, per la matematica, che individuò nel concetto di tempo per l'Aritmetica e nel concetto di spazio per la Geometria: in questo modo pensò di risolvere la questione dei fondamenti della matematica, che un secolo appresso si ripresentò in modo ancor più 
drammatico (questo errore di Kant non sembra scuotere l'impalcatura della sua teoria: che la matematica sia possibile non era in discussione, e la sua risposta era affrettata perché il nodo che lo interessava era quello della metafisica); questa concezione era così comune presso gli intellettuali del suo periodo e di quelli seguenti, che il grande Karl Friedrich Gauss (ritenuto, a ragione, il maggior matematico dei tempi moderni) pur avendo scoperto le geometrie non euclidee non volle divulgarne l'esistenza temendo "le strida dei beoti" (cioè dei filosofi idealisti che impazzavano per l'Europa in quell'epoca). Nell'ottocento la Matematica ed in particolare la Geometria, fecero passi da gigante, ma le concezioni euclidee, così radicate nell'immaginario collettivo resistettero e resistono in molti fino ai giorni nostri.
Che molti siano convinti, infatti, che la Geometria studia lo spazio, intendendo così lo spazio nel quale viviamo, l'universo, il cosmo, è cosa innegabile. Che gli astronomi ed i fisici in genere utilizzino le teorie geometriche per descrivere gli oggetti reali è senz'altro vero, ma questo non implica in alcun modo che gli oggetti geometrici, debbano per questo esistere nel nostro universo (o in qualsiasi altro).
Le figure che disegniamo su una lavagna, su un foglio o su uno schermo di computer sono ciò che dice la parola: delle figure, delle rappresentazioni, non gli oggetti stessi. La loro utilità è euristica, tutta fondata sulla potenza immaginifica che il senso della vista ha nella nostra mente, ma non è inconcepibile, e ne esistono, un libro di Geometria privo di qualsiasi tipo di figura (il grande matematico italo-francese Lagrange si vantava proprio di questo nella sua Meccanica Analitica ove spiegava il moto dei corpi, e le traiettorie degli altri senza tracciare una sola figura!). Ma spesso non è solo la figura, o il modello concreto, a fornire una illustrazione di un concetto, bensì una particolare figura o un particolare oggetto che troviamo in natura, può servire come riferimento per l'immaginazione di un nuovo concetto geometrico astratto. Un esempio illustre è quello della Geometria Proiettiva; con 
questa locuzione si designa un ramo della Geometria che studia le figure geometriche non secondo le loro relazioni euclidee (come distanze, angoli, etc.) ma vedendole come proiettate su piani. La motivazione era di natura pittorica: quando nel Rinascimento si iniziò a riscoprire la prospettiva, cioè la tecnica pittorica che consente di rappresentare un oggetto tridimensionale su un piano bidimensionale (la tela) senza "appiattirlo", alcuni maestri (come Piero della Francesca) descrissero questa tecnica e diedero il via ad una serie di ricerche, che poi nel seicento portarono Pascal e Desargues a gettare le fondamenta di un nuovo tipo di Geometria, diversa da quella Euclidea. Sostanzialmente due figure sono considerate equivalenti dal punto di vista della Geometria Proiettiva se possono essere proiettata l'una sull'altra: ad esempio un attore è proiettivamente equivalente alla sua immagine sullo schermo cinematografico!
Osserviamo che una discriminante per distinguere un tipo di concezione geometrica dall'altra è proprio l'equivalenza delle figure, cioè la differenza fra una geometria e un'altra consiste nelle differenti trasformazioni che sono ammesse per dire quando due figure sono equivalenti; questa osservazione è piuttosto recente, risalendo a Klein e Lie, due grandi matematici del diciannovesimo secolo, ed è stata la base per l'introduzione della Teoria dei Gruppi in Geometria (evento capitale sul quale però non possiamo soffermarci).
Quello che possiamo rilevare è che mentre la Geometria Euclidea deriva in qualche senso dalla capacità umana di valutare le distanza, e quindi dalla possibilità di vedere e toccare oggetti vicini a noi, quella Proiettiva deriva dalla vista a lungo raggio, dalla possibilità, ad esempio, di seguire due binari che si allontanano all'orizzonte e di notare come sembrino avvicinarsi sempre di più, mentre invece sappiamo che sono paralleli: in effetti due rette in Geometria Proiettiva, finiscono sempre per incontrarsi, mentre in Geometria Euclidea possono essere parallele.
Le concezioni geometriche sono quindi a loro volta astrazioni di osservazioni concrete, e tutti gli assiomi delle teorie geometriche potrebbero motivarsi in questo modo, o meglio potrebbe in questo modo motivarsi la loro scoperta e formulazione.
Ad esempio, una caratteristica fondamentale, messa in luce nell'antichità da Archimede e in tempi più recenti da Dedekind, cioè la continuità delle figure geometriche, deriva chiaramente dal senso del tatto. Una figura geometrica è continua nel senso che i suoi punti riempiono senza interruzioni una porzione di spazio (il grande matematico Euler, nel settecento, ancora definiva la continuità di una curva come la possibilità di poterla tracciare senza staccare la matita dal foglio) e, se immaginiamo un modello fisico del 
nostro oggetto geometrico, questo vuol dire che possiamo scorrerlo con una mano senza incontrare interruzioni, buchi, lacune. La continuità di un oggetto geometrico in qualche modo prescinde dalla vista e rappresenta una connotazione meno raffinata delle altre, proprio perché il nostro senso del tatto è meno raffinato del senso della vista. Rinunciare alle caratteristiche euclidee o proiettive non vuol dire quindi rinunciare alla continuità delle figure, e la Geometria delle figure solo continue si chiama Topologia (è un caso che uno dei maggiori topologi del nostro secolo, il russo Pontriagin, fosse cieco?). La Topologia è molto più giovane delle sue antecedenti Euclidea e Proiettiva, ed il motivo è che prima di teorizzarla bisognava liberarsi di tutte le concezioni metriche e "rigide" accumulate in millenni di storia del pensiero umano (lo psicologo Piaget ha constatato come nei bambini piccoli sia presente la concezione topologica degli oggetti più che quella euclidea: molti non distinguono bene fra un cerchio, un quadrato o un triangolo, quando gli si chiede di disegnarlo, ma distinguono fra un cerchio ed un segmento, e qui la distinzione è topologica).
Se assumiamo che l'unico concetto di equivalenza fra le figure sia quello della continuità, un oggetto topologico può deformarsi a piacimento (purché non lo si strappi o lo si tagli) senza alterare la sua natura. Così un quadrato, una calotta sferica, un disco, sono tutti equivalenti. Un quadrato non è però equivalente a un quadrato con un buco nel mezzo, perché, in prossimità del buco, la continuità viene a mancare (col tatto ci rendiamo perfettamente conto della presenza del buco, mentre nel quadrato pieno persiste).
La scoperta della Topologia (che si può far risalire al genio di Riemann, metà dell'ottocento, ma che inizia effettivamente con Poincaré agli inizi del nostro secolo) ha mostrato quanti e quali oggetti "impossibili" sia possibile concepire. La parola "impossibili" è appropriata: delle molte figure topologiche non possiamo disegnarne, né costruirne modelli tridimensionali, che per poche in modo preciso.
La costruzione di nuovi oggetti topologici è soggetta a meno vincoli di quelli euclidei, e quindi è in un certo senso più difficile: ad esempio, una qualsiasi figura che sia deformazione di un quadrato è, topologicamente, un quadrato e quindi non un oggetto realmente nuovo. La scoperta di oggetti topologicamente nuovi ha permesso di introdurre in questo mondo oggetti che di questo mondo non hanno certo l'aspetto.
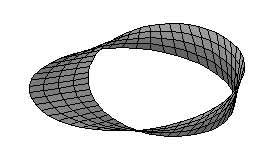
Un esempio elementare è quello del nastro di Moebius; partiamo da un suo parente che è di questo mondo, il cilindro. Per costruire un cilindro, basta prendere una striscia rettangolare (di carta, di pelle, ...) e piegarla fino a far combaciare due dei suoi lati opposti. L'operazione così compiuta crea un nuovo oggetto topologico, molto familiare. Se però, mentre pieghiamo il nastro fino a far congiungere gli estremi lo "torciamo" su se stesso (se il nastro è lungo questo non è difficile da fare) e poi ne incolliamo le estremità così storte, otteniamo un oggetto che è "circolare" così come lo è il cilindro, ma che è topologicamente diverso. Si tratta del nastro di Moebius. La diversità è topologica: il cilindro ha due bordi, cioè i due cerchi superiore e inferiore che ne delimitano la superficie; questi due cerchi si possono toccare. Se però analizziamo i bordi del nastro di Moebius ci rendiamo conto che il plurale è sbagliato: il nastro di Moebius ha solo un bordo! Se lo tocchiamo, seguendone col dito il contorno, ce ne possiamo rendere conto immediatamente; quindi il nastro di Moebius è una porzione di superficie limitata da un solo bordo (come un disco circolare) ma che, a differenza del disco circolare, che ha due lati, ha un lato solo... Per esprimere la diversità che c'è fra un nastro di Moebius e un cilindro si usa dire che il primo non è orientabile, col che vogliamo significare che non possiede nessun verso. Il cilindro ha evidentemente una parte interna ed una parte esterna, il nastro di Moebius no.
In Topologia gli oggetti non orientabili fanno legione: un esempio ancor più interessante (ed alieno) è la bottiglia di Klein. Per costruire la bottiglia di Klein si può partire da un rettangolo e formare, sempre facendo combaciare due sue estremità, il familiare cilindro. Poi, dato che siamo in Topologia, immaginiamo (o realizziamo con la gomma) che il nostro cilindro sia molto "alto", che insomma sia un tubo. Dato che è un tubo di gomma, possiamo piegarlo, fino a far combaciare i suoi bordi, che sono due cerchi. Se facciamo semplicemente questo, otteniamo una ciambella, un salvagente, che i topologi, per motivi di tradizione etimologica, chiamano "toro": questa è una figura familiare, di questo mondo. Per realizzare la bottiglia di Klein dobbiamo invece "torcere" il tubo prima di farne combaciare le estremità, esattamente come abbiamo fatto per il nastro di Moebius. Questa operazione non può farsi nel nostro universo, a meno di non riuscire a far compenetrare il tubo in se stesso, ed in effetti le immagini della bottiglia di Klein che possiamo realizzare ci mostrano delle "intersezioni" dell'oggetto con se stesso, dovute alla sua estraneità a questo mondo. Un modo equivalente di vedere la bottiglia di Klein è considerare tubo la cui sezione non sia circolare, ma sia un "otto", cioè una coppia di cerchi uniti in un punto. A questo punto storcendo il tubo prima di far combaciare le estremità, otteniamo di nuovo la nostra bottiglia di Klein. Il perché si chiami bottiglia, è dovuto al fatto che Klein immaginava il tubo come il collo di una bottiglia; ma il suo arcano contenitore, non avendo né interno né esterno, sarebbe poco adatto a stipare liquidi di questo mondo.
La pervasività della Topologia nella scienza moderna è impressionante: la Fisica, a tutti i livelli, dalla Teoria delle Particelle Elementari alla Cosmologia, ne fa un uso massiccio.
Un fatto che può apparire bizzarro, nella storia del pensiero scientifico moderno, è che mentre la Matematica scopriva in tutto il suo splendore la continuità, con la nascita della Topologia, la Fisica scopriva la discontinuità: la scoperta degli atomi, del fatto che le figure che ci sembrano (al tatto, appunto) continue in realtà sono costituite da una teoria fittissima di particelle discrete, sembra dover presagire l'inadeguatezza dei modelli geometrici (che sono tutti continui) in ambito fisico. Sorprendentemente è vero il viceversa.
Una caratteristica degli oggetti, una volta che siano visti con gli occhi del topologo, è che possono essere concepiti in modo intrinseco, cioè non immersi in uno spazio ulteriore, come accadeva in genere per gli oggetti della Geometria Euclidea. Anzi, lo spazio stesso diviene un oggetto geometrico, suscettibile di studio nella sua totalità.
Nella Teoria di Einstein della Relatività Generale, ad esempio, lo spazio non è necessariamente piatto, ma può avere una curvatura, così come una sfera o un iperboloide; l'analogia è completa, a parte il fatto che una sfera e un iperboloide sono superfici, cioè oggetti a due dimensioni, mentre l'universo della Relatività ne ha quattro (le tre spaziali ed il tempo).
Il problema della tridimensionalità dello spazio (che, a quanto pare, molti fisici contemporanei mettono in discussione) non è così banale come potrebbe sembrare. Il concetto stesso di dimensione è una acquisizione recente, in gran parte dovuta al matematico francese Legesbue, ed è un concetto, nella sua generalità, topologico. L'affermazione "lo spazio ha tre dimensioni", anche assumendo come modello per lo spazio uno degli oggetti contemplati dalla Topologia, è tutt'altro che facile da spiegare. Eppure, la tridimensionalità sembra essere un dato ricorrente in tutti gli oggetti matematici che ammettono modelli spaziali, concreti. Ad esempio, da millenni l'uomo conosce i nodi, li usa e li studia: i marinai ne conoscono molti diversi, e quindi sanno bene che ci sono nodi non equivalenti fra loro dal punto di vista topologico: ci sono nodi molto complicati che però, tirandone le due estremità della corda che li realizza, si sciolgono; altri no. Una classificazione completa dei nodi non esiste a tutt'oggi, e per distinguere nodi non equivalenti sono stati introdotti degli invarianti matematici estremamente complicati (negli anni '90 il matematico statunitense Vaughan Jones ha definito dei polinomi che consentono una classificazione molto raffinata, se non definitiva, dei nodi).
Ma, si dimostra, in uno spazio con più di tre dimensioni, ogni nodo si può sciogliere. Questo è un teorema topologico molto interessante: ne esistono di simili che sanciscono come proprietà geometriche cruciali siano significative esattamente in dimensione tre; e la cosa ancor più interessante è che la teoria dei nodi ha delle conseguenze notevolissime su certe moderne teorie quantistiche, perché taluni modelli della Fisica moderna, come le cosiddette stringhe, sono descritti in termini della geometria dei nodi e delle loro simmetrie.
Non è possibile qui affrontare la questione della tridimensionalità dello spazio; possiamo limitarci ad osservare che due dimensioni sembrano essere troppo poche, mentre quattro sono già troppe. Ad esempio, in un mondo bidimensionale (come quello concepito da Abbot nel suo romanzo Flatlandia) sarebbe impossibile lo sviluppo di esseri viventi, almeno nel senso che noi attribuiamo alla parola. Proviamo ad immaginare un animale in due dimensioni; come farebbe a nutrirsi? la presenza di un tubo digerente implica la tridimensionalità, dato che in una figura bidimensionale, un tubo digerente che la attraversasse, la renderebbe non connessa come dicono i topologi, cioè composta di due parti separate... In generale, più dimensioni possiede un oggetto geometrico, più è facile spostarsi in esso, tanto è vero che i Fisici chiamano le dimensioni: gradi di libertà. Ma, come l'esempio dei nodi ci mostra, in un mondo con più di tre dimensioni, ci sarebbe forse troppa libertà di movimento: si potrebbero fare troppe cose, e i costituenti della materia avrebbero troppa libertà di movimento per realizzare effettivamente le strutture atomiche, molecolari e biologiche che compongono il nostro mondo e noi stessi.
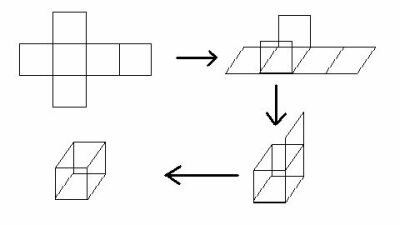
Naturalmente i matematici non possono certo lasciarsi frenare da queste obiezioni nelle loro indagini: vediamo ad esempio come possiamo rappresentare un oggetto a quattro dimensioni, precisamente un ipercubo. Tutti sanno come sia fatto un cubo, e molti saprebbero anche costruirlo con carta, matita e forbici: si disegnano sei quadrati contigui su un foglio, si ritaglia la loro sagoma complessiva e si ripiega la figura piana facendo combaciare i bordi dei quadrati ed ottenendo il cubo. In modo analogo, se prendiamo la stessa figura piana, composta di quadrati, che dà luogo, dopo il ripiegamento al cubo, e su ognuno dei quadrati mettiamo un cubo, immaginando di chiudere questo oggetto così come chiuderemmo i quadrati per ottenere un cubo, otteniamo un ipercubo; ovviamente in questo mondo la cosa non può farsi, a meno di non compenetrare la materia in se stessa. Possiamo però, distorcendo le distanze, persino disegnare in due dimensioni la proiezione tridimensionale dell'ipercubo.
Per chi volesse avere una visione animata e tridimensionale dell'ipercubo lascio un collegamento alla pagina Stereoscopic Animated Hypercube che contiene uno script Java con una animazione; inoltre si può scaricare il programma shareware di Rudy Rucker qui dalla mia pagina. Animazioni della bottiglia di Klein si trovano sulla pagina di Thomas Banchoff, mentre informazioni sui nodi si possono trovare in questa pagina.
